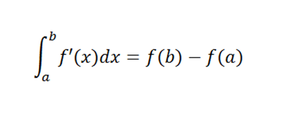AP Calculus
Course Overview
We cover everything in the Calculus AB topic outline as it appears in the AP Calculus Course Description. We will also cover some additional topics after the AP exam is completed. The list includes: integration by parts, partial fractions, and integral tables. The primary textbook is Calculus: Graphical, Numerical, Algebraic, by Ross Finney, Franklin Demana, Bert Waits, and Daniel Kennedy.
Course Planner
Below is the sequence of our AP Calculus AB course. We will try to follow this timeline as close as possible, but there might be some slight variations depending on class understanding. This timeline will give us approximately 15 days to review the course for the AP exam.
First Semester AP Calculus AB
|
Chapter 1
1.1 1.2 1.3 1.4 1.5 1.6 |
Prerequisites for Calculus
Lines Functions and Graphs Exponential Functions Quiz 1.1-1.3 Parametric Equations Functions and Logarithms Trigonometric Functions Review Exercises/Test |
Timeline
1 day 2 days 1 day 1 day 2 days 1 day 2 days 2 days |
|
Chapter 2
2.1 2.2 2.3 2.4 |
Limits and Continuity
Rates of Change and Limits Limits Involving Infinity Quiz 2.1-2.2 Continuity Rates of Change and Tangent Lines Review Exercises/Test |
Timeline
2 days 2 days 1 day 2 days 2 days 2 days |
|
Chapter 3
3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 |
Derivatives
Derivative of a Function Differentiability Rules of Differentiation Quiz 3.1-3.3 Velocity and Other Rates of Change Derivatives of Trigonometric Functions Chain Rule Quiz 3.4-3.6 Implicit Differentiation Derivatives of Inverse Trigonometric Functions Derivatives of Exponential and Logarithmic Functions Review Exercises/Test |
Timeline
3 days 3 days 3 days 1 day 3 days 3 days 3 days 1 day 2 days 2 days 3 days 2 days |
|
Chapter 4
4.1 4.2 4.3 4.4 4.5 4.6 |
Applications of Derivatives
Extreme Values of Functions Mean Value Theorem Connecting f’ and f” with the Graph of f Quiz 4.1-4.3 Modeling and Optimization Linearization (and Newton’s Method optional) Related Rates Review Exercises/Test |
Timeline
3 days 2 days 4 days 1 day 3 days 3 days 3 days 2 days |
Semester Exam- Chapters 1-4
|
Chapter 5
5.1 5.2 5.3 5.4 5.5 |
The Definite Integral
Estimating with Finite Sums Definite Integrals Definite Integrals and Antiderivatives Quiz 5.1-5.3 Fundamental Theorem of Calculus Trapezoidal Rule Review Exercises/Test |
Timeline
3 days 3 days 4 days 1 day 4 days 2 days 2 days |
|
Chapter 6
6.1 6.2 6.4 6.5 6.6 |
Differential Equations and Mathematical Modeling
Antiderivatives and Slope Fields Integration by Substitution Quiz 6.1-6.2 Exponential Growth and Decay Population Growth Numerical Methods Review Exercises/Test |
Timeline
3 days 3 days 1 day 3 days 3 days 3 days 2 days |
|
Chapter 7
7.1 7.2 7.3 7.4 7.5 |
Applications of Definite Integrals
Integral as Net Change Areas in the Plane Volumes Quiz 7.1-7.3 Lengths of Curves Applications from Science and Statistics Review Exercises/Test |
Timeline
4 days 3 days 4 days 1 day 4 days 4 days 2 days |
|
Chapter 8
8.1 |
L'Hopital's Rule
L'Hopital's Rule |
Timeline
2 days |
Review for AP Exam
|
15 days
|
After the AP Exam
|
6.3
8.4 |
Integration by Parts
Partial Fractions and Integral Tables |
3 day
2 days |
Teacher Resources
Primary Textbook
Finney, Demana, Waits, and Daniel Kennedy. Calculus: Graphical, Numerical, Algebraic. New Jersey: Pearson Education, Inc., 2003.
Finney, Demana, Waits, and Daniel Kennedy. Calculus: Graphical, Numerical, Algebraic. New Jersey: Pearson Education, Inc., 2003.
Technology and Computer Software
Teacher will be using TI-84 Plus graphing calculator overhead projector for class presentations. Almost all students use a TI-83, TI-83 Plus, TI-84, or TI-84 Plus graphing calculator. Calculators are a major focus for the class. Students are expected to graph a function in a specified window, use a table to support conclusions, approximate the derivative at a point, and approximate the value of a definite integral.
Teacher will also use an LCD projector for PowerPoint presentations, software by Geometer’s Sketchpad, and TI-InterActive! to aid in the teaching of many calculus concepts.
Teacher will also use an LCD projector for PowerPoint presentations, software by Geometer’s Sketchpad, and TI-InterActive! to aid in the teaching of many calculus concepts.
Teaching Strategies
Calculus ideas are presented and investigated graphically, numerically, and algebraically. Students are expected to be able to relate the various representations to each other. Students are also expected to understand that verification is only done by algebraic means.
Communicating mathematically is a major goal for this course. Students are asked question daily and are expected to be able to explain the problems using the proper vocabulary and terms. Students are also asked to go to the board and explain solutions to their classmates.
Communicating mathematically is a major goal for this course. Students are asked question daily and are expected to be able to explain the problems using the proper vocabulary and terms. Students are also asked to go to the board and explain solutions to their classmates.
Student Evaluation
Starting in January, I will assign one AP free response question for the students to work on for three days. In February, students will be given two days and in March students will be given one day. This will continue until the AP examination in the beginning of May. These will be graded as quizzes and students can work individually or in groups and can use their books or come to me for extra help. Students are graded as they would be graded on the AP Exam. (Free-response questions and scoring guidelines are available on AP Central.)
Starting in December, I will start giving the students multiple choice problems off the AP Calculus Released Exams. Two questions will be put up on the LCD projector at the start of each class and will continue until the AP examination. Three weeks prior to the exam, students will be given full multiple choice sections of the AP Calculus Released Exams and they will be timed. Students will be given non-calculator and calculator sections as to familiarize them with the AP Exam format. This has always proven to be a good way to review and get students ready for what they can expect to see on the AP Exam.
Starting in December, I will start giving the students multiple choice problems off the AP Calculus Released Exams. Two questions will be put up on the LCD projector at the start of each class and will continue until the AP examination. Three weeks prior to the exam, students will be given full multiple choice sections of the AP Calculus Released Exams and they will be timed. Students will be given non-calculator and calculator sections as to familiarize them with the AP Exam format. This has always proven to be a good way to review and get students ready for what they can expect to see on the AP Exam.
Student Activities
Throughout the course there will be a variety of activities on the CBL (Texas Instruments’ Calculator-Based Laboratory). An example is a motion detector is used to plot distance versus time. Students will be able to gain a better understanding of how the displacement curve is related to the velocity curve.
There will also be Geometer’s Sketchpad activities on change, limits, derivatives, anti-derivatives, and integrals.
There will also be Geometer’s Sketchpad activities on change, limits, derivatives, anti-derivatives, and integrals.
Grading
Your grade will be based upon written exams, tests, quizzes, writing assignments, homework, class participation, and creativity.
Exams and Quizzes:
Everyone will take the midterm and final. Some senior exemptions apply.
You can expect a variety of types of questions on your exams and quizzes. Most questions will ask you to provide an explanation for your answer. In this explanation you may include diagrams and computation. I will be looking for the correct use of the mathematical terminology.
Exams and quizzes will be graded with little partial credit. However you will be allowed to earn 1/3 of the points you lost back if you do the following.
Test Correction Procedure
1) Rewrite the question you got wrong.
2) Provide a complete correct answer. You must convince me that you now understand your mistakes.
3) If the question was a true/false variety or a definition, you must write out the definition, theorem, or postulate that will justify your answer.
4) Next to each question write down the amount of the points you lost.
5) Attach this to your exam and turn in on the day it is due. It will not be accepted late.
6) The corrections must be neat and easy to read.
7) You may use your notes, text, me or get help from a friend. Just make sure you learn from your mistakes.
Example:
Solve the following. 3X - 4 = 5
3X = 1
X = 1/3 incorrect
Correction:
Solve the following: 3X - 4 = 5
3X - 4 = 5
+4 +4 Note: I subtracted 4 from 5 in my original solution.
3X = 9
X = 3
3(3) - 4 = 5
9 - 4 = 5
5 = 5 Check
Homework:
Homework is an extremely important part of any mathematics course. As practice in sports or music sharpens your skills so does homework sharpen your mathematical skills. I will choose specific problems that will sharpen your skills.
Homework will be graded in three ways (completely done, ½ done, and not done). This is how I will grade homework for a nine-week period. I will calculate all incomplete assignments.
0 to 1 incomplete assignments result in a 10 out of 10 for a homework grade.
1&1/2 incomplete assignments result in a 9 out of 10 for a homework grade.
2 incomplete assignments result in an 8 out of 10 for a homework grade.
2&1/2 incomplete assignments result in a 7 out of 10 for a homework grade.
3 incomplete assignments result in a 6 out of 10 for a homework grade.
3&1/2 incomplete assignments result in a 5 out of 10 for a homework grade.
4 incomplete assignments result in a 4 out of 10 for a homework grade.
This pattern continues until a 0 out of 10 for a homework grade.
Everyone should end up with 10% of his or her grade being an A.
* The homework policy may change during the semester.
EXTRA CREDIT will rarely occur. When it does it will be directly related to the work we are doing. You will not be able to pass this class with extra credit.
Grading (nine weeks): Semester:
Tests – 45% First nine weeks- 40%
Quizzes and writing assignments - 40% Second nine weeks- 40%
Homework- 10% Semester exam- 20%
Class participation and creativity - 5%
94-100% A 73-76% C
90-93% A- 70-72% C-
87-89% B+ 67-69% D+
83-86% B 63-66% D
80-82% B- 60-62% D-
77-79% C+ 0-59% F
Cheating:
If you are caught cheating you will FAIL that test, quiz, etc. In order to pass the semester you must work very hard for the remainder of the semester to pass. Please do not put yourself in this situation. I would rather have you fail than cheat. If you fail, redemption is always possible.
Supplies:
3-ring binder folder
paper for homework (some may choose to use graphing paper)
graphing calculator (TI-84 Family of calculators)
If you have any concerns, questions etc., please feel free to talk with me about them. There is always something we can work out. It is never too late to improve.
Exams and Quizzes:
Everyone will take the midterm and final. Some senior exemptions apply.
You can expect a variety of types of questions on your exams and quizzes. Most questions will ask you to provide an explanation for your answer. In this explanation you may include diagrams and computation. I will be looking for the correct use of the mathematical terminology.
Exams and quizzes will be graded with little partial credit. However you will be allowed to earn 1/3 of the points you lost back if you do the following.
Test Correction Procedure
1) Rewrite the question you got wrong.
2) Provide a complete correct answer. You must convince me that you now understand your mistakes.
3) If the question was a true/false variety or a definition, you must write out the definition, theorem, or postulate that will justify your answer.
4) Next to each question write down the amount of the points you lost.
5) Attach this to your exam and turn in on the day it is due. It will not be accepted late.
6) The corrections must be neat and easy to read.
7) You may use your notes, text, me or get help from a friend. Just make sure you learn from your mistakes.
Example:
Solve the following. 3X - 4 = 5
3X = 1
X = 1/3 incorrect
Correction:
Solve the following: 3X - 4 = 5
3X - 4 = 5
+4 +4 Note: I subtracted 4 from 5 in my original solution.
3X = 9
X = 3
3(3) - 4 = 5
9 - 4 = 5
5 = 5 Check
Homework:
Homework is an extremely important part of any mathematics course. As practice in sports or music sharpens your skills so does homework sharpen your mathematical skills. I will choose specific problems that will sharpen your skills.
Homework will be graded in three ways (completely done, ½ done, and not done). This is how I will grade homework for a nine-week period. I will calculate all incomplete assignments.
0 to 1 incomplete assignments result in a 10 out of 10 for a homework grade.
1&1/2 incomplete assignments result in a 9 out of 10 for a homework grade.
2 incomplete assignments result in an 8 out of 10 for a homework grade.
2&1/2 incomplete assignments result in a 7 out of 10 for a homework grade.
3 incomplete assignments result in a 6 out of 10 for a homework grade.
3&1/2 incomplete assignments result in a 5 out of 10 for a homework grade.
4 incomplete assignments result in a 4 out of 10 for a homework grade.
This pattern continues until a 0 out of 10 for a homework grade.
Everyone should end up with 10% of his or her grade being an A.
* The homework policy may change during the semester.
EXTRA CREDIT will rarely occur. When it does it will be directly related to the work we are doing. You will not be able to pass this class with extra credit.
Grading (nine weeks): Semester:
Tests – 45% First nine weeks- 40%
Quizzes and writing assignments - 40% Second nine weeks- 40%
Homework- 10% Semester exam- 20%
Class participation and creativity - 5%
94-100% A 73-76% C
90-93% A- 70-72% C-
87-89% B+ 67-69% D+
83-86% B 63-66% D
80-82% B- 60-62% D-
77-79% C+ 0-59% F
Cheating:
If you are caught cheating you will FAIL that test, quiz, etc. In order to pass the semester you must work very hard for the remainder of the semester to pass. Please do not put yourself in this situation. I would rather have you fail than cheat. If you fail, redemption is always possible.
Supplies:
3-ring binder folder
paper for homework (some may choose to use graphing paper)
graphing calculator (TI-84 Family of calculators)
If you have any concerns, questions etc., please feel free to talk with me about them. There is always something we can work out. It is never too late to improve.
AP Calculus Philosophy
Calculus AB is primarily concerned with developing the students' understanding of the concepts of calculus and providing experience with its methods and applications. The course emphasizes a multi-representational approach to calculus, with concepts, results, and problems being expressed geometrically, numerically, analytically, and verbally. The connections among these representations also are important.
Broad concepts and widely applicable methods are emphasized. The focus of the course is neither manipulation nor memorization of an extensive taxonomy of functions, curves, theorems, or problem types. Thus, although facility with manipulation and computational competence are important outcomes, they are not the core of this course.
Technology is used regularly by students and teachers to reinforce the relationships among the multiple representations of functions, to confirm written work, to implement experimentation, and to assist in interpreting results.
Through the use of the unifying themes of derivatives, integrals, limits, approximation, and applications and modeling, the course becomes a cohesive whole rather than a collection of unrelated topics.
Broad concepts and widely applicable methods are emphasized. The focus of the course is neither manipulation nor memorization of an extensive taxonomy of functions, curves, theorems, or problem types. Thus, although facility with manipulation and computational competence are important outcomes, they are not the core of this course.
Technology is used regularly by students and teachers to reinforce the relationships among the multiple representations of functions, to confirm written work, to implement experimentation, and to assist in interpreting results.
Through the use of the unifying themes of derivatives, integrals, limits, approximation, and applications and modeling, the course becomes a cohesive whole rather than a collection of unrelated topics.
The Goals of AP Calculus
Students should be able to:
• work with functions represented in a variety of ways: graphical, numerical, analytical, or verbal. They should understand the connections among these representations.
• understand the meaning of the derivative in terms of a rate of change and local linear approximation and they should be able to use derivatives to solve a variety of problems.
• understand the meaning of the definite integral both as a limit of Riemann sums and as the net accumulation of a rate of change and should be able to use integrals to solve a variety of problems.
• understand the relationship between the derivative and the definite integral as expressed in both parts of the Fundamental Theorem of Calculus.
• communicate mathematics both orally and in well-written sentences and should be able to explain solutions to problems.
• model a written description of a physical situation with a function, a differential equation, or an integral.
• use technology to help solve problems, experiment, interpret results, and verify conclusions.
• determine the reasonableness of solutions, including sign, size, relative accuracy, and units of measurement.
• develop an appreciation of calculus as a coherent body of knowledge and as a human accomplishment.
• work with functions represented in a variety of ways: graphical, numerical, analytical, or verbal. They should understand the connections among these representations.
• understand the meaning of the derivative in terms of a rate of change and local linear approximation and they should be able to use derivatives to solve a variety of problems.
• understand the meaning of the definite integral both as a limit of Riemann sums and as the net accumulation of a rate of change and should be able to use integrals to solve a variety of problems.
• understand the relationship between the derivative and the definite integral as expressed in both parts of the Fundamental Theorem of Calculus.
• communicate mathematics both orally and in well-written sentences and should be able to explain solutions to problems.
• model a written description of a physical situation with a function, a differential equation, or an integral.
• use technology to help solve problems, experiment, interpret results, and verify conclusions.
• determine the reasonableness of solutions, including sign, size, relative accuracy, and units of measurement.
• develop an appreciation of calculus as a coherent body of knowledge and as a human accomplishment.
AP Calculus --
Topical Outlines
I. Functions, Graphs, and Limits
Analysis of graphs. With the aid of technology, graphs of functions are often easy to produce. The emphasis is on the interplay between the geometric and analytic information and on the use of calculus both to predict and to explain the observed local and global behavior of a function.
Limits of functions (including one-sided limits).
II. Derivatives
Concept of the derivative.
III. Integrals
Interpretations and properties of definite integrals.
Analysis of graphs. With the aid of technology, graphs of functions are often easy to produce. The emphasis is on the interplay between the geometric and analytic information and on the use of calculus both to predict and to explain the observed local and global behavior of a function.
Limits of functions (including one-sided limits).
- An intuitive understanding of the limiting process.
- Calculating limits using algebra.
- Estimating limits from graphs or tables of data.
- Understanding asymptotes in terms of graphical behavior.
- Describing asymptotic behavior in terms of limits involving infinity.
- Comparing relative magnitudes of functions and their rates of change. (For example, contrasting exponential growth, polynomial growth, and logarithmic growth.)
- An intuitive understanding of continuity. (Close values of the domain lead to close values of the range.)
- Understanding continuity in terms of limits.
- Geometric understanding of graphs of continuous functions (Intermediate Value Theorem and Extreme Value Theorem).
II. Derivatives
Concept of the derivative.
- Derivative presented geometrically, numerically, and analytically.
- Derivative interpreted as an instantaneous rate of change.
- Derivative defined as the limit of the difference quotient.
- Relationship between differentiability and continuity.
- Slope of a curve at a point. Examples are emphasized, including points at which there are vertical tangents and points at which there are no tangents.
- Tangent line to a curve at a point and local linear approximation.
- Instantaneous rate of change as the limit of average rate of change.
- Approximate rate of change from graphs and tables of values.
- Corresponding characteristics of graphs of f and f'.
- Relationship between the increasing and decreasing behavior of f and the sign of f'.
- The Mean Value Theorem and its geometric consequences.
- Equations involving derivatives. Verbal descriptions are translated into equations involving derivatives and vice versa.
- Corresponding characteristics of the graphs of f, f', and f".
- Relationship between the concavity of f and the sign of f".
- Points of inflection as places where concavity changes.
- Analysis of curves, including the notions of monotonicity and concavity.
- Optimization, both absolute (global) and relative (local) extrema.
- Modeling rates of change, including related rates problems.
- Use of implicit differentiation to find the derivative of an inverse function.
- Interpretation of derivative as a rate of change in varied applied contexts, including velocity, speed, and acceleration.
- Knowledge of derivatives of basic functions, including power, exponential, trigonometric, and inverse trigonometric functions.
- Basic rules for the derivative of sums, products, and quotients of functions.
- Chain Rule and implicit differentiation.
III. Integrals
Interpretations and properties of definite integrals.
- Computation of Riemann sums using left, right and midpoint evaluation points.
- Definite integral as a limit of Riemann sums over equal subdivisions.
- Definite integral of the rate of change of a quantity over an interval interpreted as the change of the quantity over the interval:
Basic properties of definite integrals. (Examples include additivity and linearity.)
Applications of integrals. Appropriate integrals are used in a variety of applications to model physical, social, or economic situations. Although only a sampling of applications can be included in any specific course, students should be able to adapt their knowledge and techniques to solve other similar application problems. Whatever applications are chosen, the emphasis is on using the integral of a rate of change to give accumulated change or using the method of setting up an approximating Riemann sum and representing its limit as a definite integral. To provide a common foundation, specific applications should include finding the area of a region (including a region bounded by polar curves for BC only), the volume of a solid with known cross sections, the average value of a function, the distance traveled by a particle along a line, and for BC only the length of a curve (including a curve given in parametric form).
Fundamental Theorem of Calculus.
Applications of integrals. Appropriate integrals are used in a variety of applications to model physical, social, or economic situations. Although only a sampling of applications can be included in any specific course, students should be able to adapt their knowledge and techniques to solve other similar application problems. Whatever applications are chosen, the emphasis is on using the integral of a rate of change to give accumulated change or using the method of setting up an approximating Riemann sum and representing its limit as a definite integral. To provide a common foundation, specific applications should include finding the area of a region (including a region bounded by polar curves for BC only), the volume of a solid with known cross sections, the average value of a function, the distance traveled by a particle along a line, and for BC only the length of a curve (including a curve given in parametric form).
Fundamental Theorem of Calculus.
- Use of the Fundamental Theorem to evaluate definite integrals.
- Use of the Fundamental Theorem to represent a particular antiderivative, and the analytical and graphical analysis of functions so defined.
- Antiderivatives following directly from derivatives of basic functions.
- Antiderivatives by substitution of variables (including change of limits for definite integrals).
- Finding specific antiderivatives using initial conditions, including applications to motion along a line.
- Solving separable differential equations and using them in modeling. In particular, studying the equation y' = ky and exponential growth.